Frage H.J.M zum Foucault-Pendel:
mir ist zum Thema Planetenbewegung und der Mechanik der Körper noch eine Frage in den Sinn gekommen, die auch meinen Sohn nach einer Besichtigung des Foucaultschen Pendels in Paris beschäftigte. Das Pendel schwingt (gemäß dem freien Fall) und die Erde dreht sich unter der Schwingungsachse langsam unabhängig weiter. Die Markierungen unter der Kugel zeigt die verstrichene Zeit an. Nach genau 1 Tag, also 24 h müsste eigentlich die Schwingungsachse wieder der ursprünglichen entsprechen (360 Grad Umlauf der Erde um die eigene Achse). Dies ist aber auch auf der Markierungsscheibe darunter ersichtlich nicht der Fall. Hängt dies mit den nicht idealtypischen Verhältnissen zusammen (Reibungsverluste)?

Antwort:
Die Drehung der Pendelebene wird durch die sogenannte Corioliskraft verursacht. Zum deren Verständnis ist es vorteilhaft, sich zuerst die Grenzsituationen anzusehen:
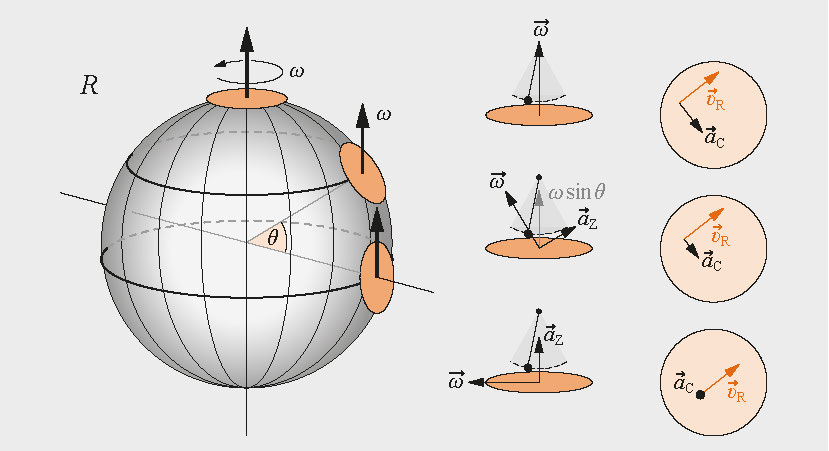
Am Nord-/Südpol: Die Erdedreht sich unter dem Pendel hinweg. Der Beobachter (Sie, s. Bild unten) denkt, das Pendel würde bei jeder Auslenkung etwas abgelenkt. Deshalb sprechen wir von einer "Scheinkraft". Nach einem Tag ist die Ausgangssituation, dieselbe Schwingunsgebene wieder erreicht. Die Drehtrate ist also R = 1/Tag = 15o h-1 Am Äquator: Das Pendel bewegt sich mit der Oberfläche entlang des Äquators. Der Beobachter sieht keine Ablenkung, die Drehrate ist R = 0. In Bonn/Paris: Die Drehrate hängt vom Winkel, d.h. vom Breitengrad mit dem Faktor sin(Breitengrad), also Bonn/Paris 51o/49o). Dann ist R = sin(51o)x15o/h = 12o h-1. Am Äquator gilt sin(0o)=0, an den Polen sin(90o)=1. Also passt unser Modell!
Die Erklärung: Die Coriolisbeschleunigung aC (scharzer Pfeil in der rechten Bildspalte (der aZ-Pfeil gilt der Zentrifugalbeschleunigung, die wir hier ignorieren) wirkt senkrecht zur Drehachse der Erde (w in der Zeichnung). Die Reibung spielt dabei keine Rolle. Sie tritt natürlich auf, wird aber duch spezielle Pendelaufhängungen und ggf. elektronische Antriebe beim Foucault-Pendel reduziert bzw. ausgeglichen.