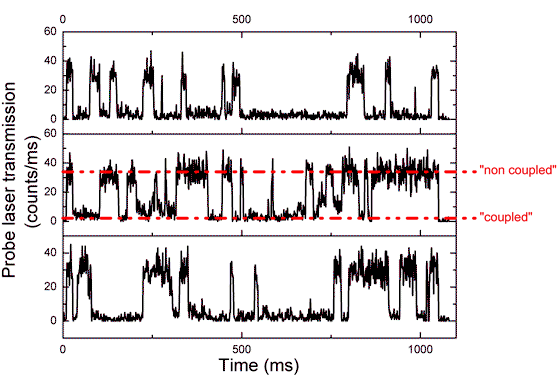
Cesium has two long-lived hyperfine ground-states. Choosing the frequency of the probe laser and the length of the cavity correctly we can couple one ground-state to the cavity field. An atom being in this coupled gound-state will reduce the probe laser transmission while an atom in the other (non coupled) ground-state will not affect the probe transmission. Via a quantum nondemolition measurement we can deduce the spin state of the atom by looking at the transmitted probe light.
We can design our system such that one atom randomly jumps from the coupled to the non coupled state by cyclic photon scattering processes. This leads to so called quantum jumps and random telegraph signals in the probe laser transmission (see following data).
When we couple two atoms to the cavity field the system becomes more interesting. With a proper choice of settings we can distinguish between three cases:
-
no atom couples ⇒ full transmission
-
one atom couples ⇒ intermediate transmission
-
both atoms couple ⇒ low transmission
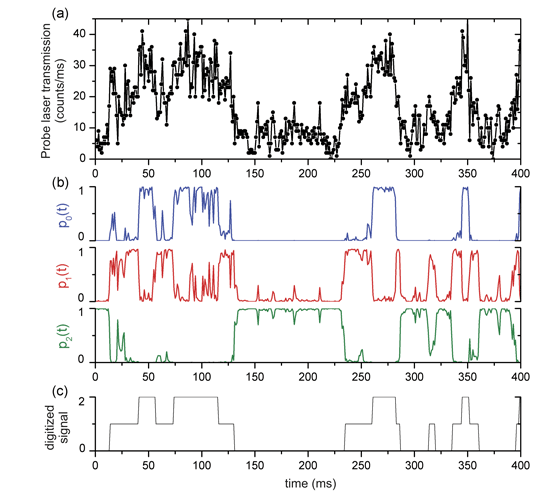
The data below (
part a) of the figure) shows a typical transmission trace when two atoms undergo quantum jumps inside our cavity.
From the data it becomes clear that the three described cases cannot be distinguished as easily as in the one atom case. One major factor that causes noise in the two-atom-case is the thermal movement of the atoms in the cavity field which leads to a variation in the coupling strength and therefore in the measured transmission.
However we can extract the maximum information from our system by employing a Bayesian update formalism which yields time-dependent probabilities for the atoms to be in the coupled or non coupled states. Part b) of the figure shows the result of such an analysis where pi(t) denotes the probability to have i atoms in the coupled state. Part c) shows a digitized version of the data which can be concluded from part b).
Read here how we use the knowledge gained from the Bayesian update formalism to manipulate the spin states of the atoms at will by a feedback loop.