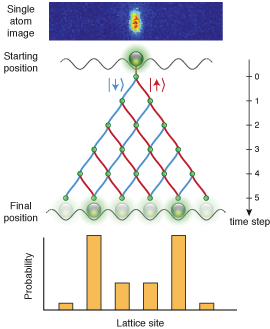
Discrete-time Quantum Walk
Quantum walks are the quantum mechanical analogue of classical random walk where the position of the walker is described by a probability distribution. This probability distribution of positions in the classical random walk is replaced by quantum mechanical superpositions in the quantum walk. Quantum mechanical interference can lead to a faster spreading of the final position distribution which can also bee seen as a faster information spreading.
One can further distinguish between discrete-time and continuous-time quantum walks. Continuous-time quantum walks are characterized by a continuous evolution of the system whereas a discrete-time quantum walk can be separated in a repeated application of two operations called "coin" (acting on the state) and "shift" (acting on the position) reminding of gate operations in quantum information processing.
The behaviour of the quantum walks be then be influenced by a proper choice of the coin and shift operation.
We realize discrete-time quantum walks by neutral Cs atoms in the hyperfine ground states which are coherently manipulated by microwave pulses (for coin operations) and moved by a well-controlled state-dependent optical lattice (for shift operations) in one dimension and are currently working on a new two-dimensional experiment.
A two-dimensional quantum walk will allow us to simulate the dispersion relation of graphene as well as artificial gauge fields during the presence of an additional polarization gradient.






 Discrete-time Quantum Walks
Discrete-time Quantum Walks

